Reële getallestelsel

ʼn Getallestelsel is ʼn sisteem of stelsel wat ons in staat stel om getalle op ʼn sekere manier uit te druk. Dit is dus ʼn wiskundige notasie om getalle voor te stel deur syfers en ander simbole op ʼn spesifieke manier te gebruik. Getallestelsels gee ons ook ʼn standaardmanier om syfers voor te stel, sodat bewerkings soos optel, aftrek, vermenigvuldiging en deling moontlik is. Dit gee ons dus ʼn manier om by standaardantwoorde uit te kom.

Die getallestelsel waarna ons in hierdie artikel gaan kyk, is die reële getallestelsel.

Hierdie stelsel kan soos volg voorgestel word: ¹

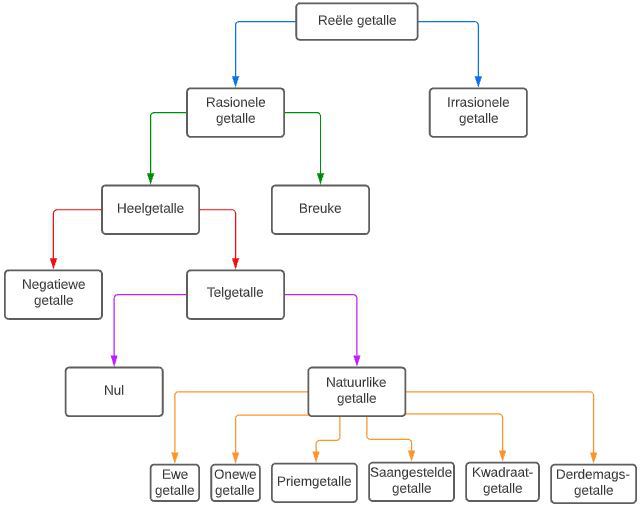
Reële getalle

Reële getalle is alle getalle wat ons in die regte wêreld gebruik; hierdie getalle kan in breuk- of desimale vorm wees. Dit sluit ook alle heelgetalle, sowel as irrasionale getalle, in. Reële getalle word verder in rasionele en irrasionele getalle verdeel. ²

Irrasionele getalle

Irrasionele getalle is getalle wat nie as gewone of onegte breuke geskryf kan word nie. Irrasionele getalle is getalle wat ons in die werklike lewe gereeld gebruik, maar hul het oneindige desimale plekke. ʼn Voorbeeld van so ʼn getal is  (pi). Dit is nie moontlik om   as ʼn gewone of onegte breuk te skryf nie. Daar is gevalle waar ons gebruik, maar hierdie breuk is nie 100% dieselfde as  nie. Wanneer ons tot die naaste vyf desimale afrond, skryf ons dit as: 3,14159, terwyl  afgerond tot die naaste vyf desimale plekke, gelyk is aan 3,14286. Ons kan sien dit is baie naby aan dieselfde getal, maar nie heeltemal dieselfde nie. Daarom sê ons dat  ʼn voorbeeld van ʼn irrasionele getal is. ²

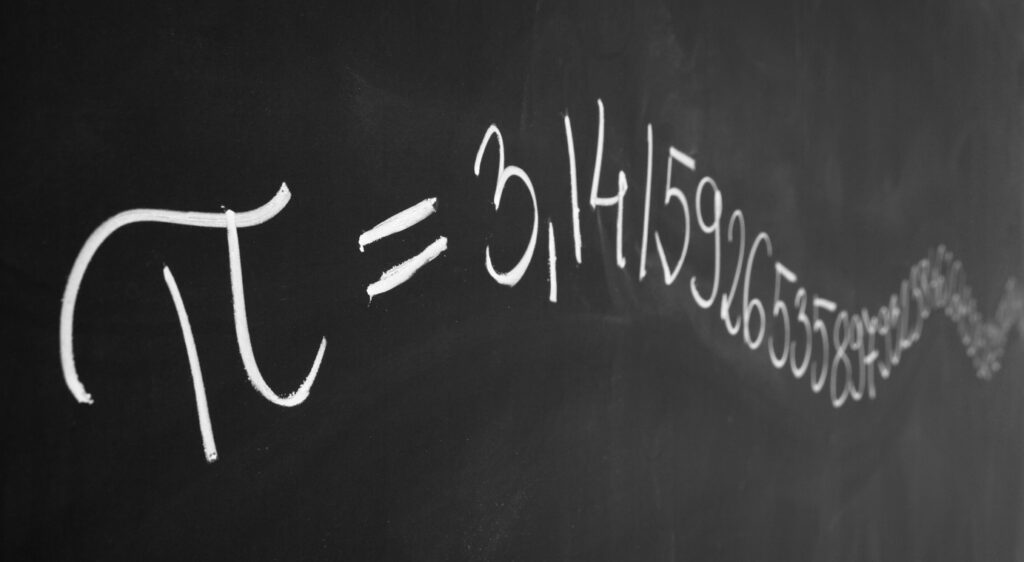
Rasionele getalle

ʼn Rasionele getal is ʼn getal wat as ʼn breuk beskryf kan word. Solank as wat die breuk ʼn eindigende of repeterende desimaal het, is dit ʼn rasionele getal. Onthou ook dat alle heelgetalle ook as breuke geskryf kan word. Rasionele getalle kan dus verder verdeel word in breuke en heelgetalle. ²

Breuke

Breuke is die getalle wat tussen heelgetalle lê. ʼn Breuk kan gedefinieer word as ʼn gedeelte van ʼn heelgetal. Wanneer ons heelgetalle gelykop verdeel, eindig ons op met breuke. Dit is belangrik om te onthou dat heelgetalle ook negatiewe getalle insluit; breuke kan dus ook negatief wees. Breuke kan in verskillende vorms voorgestel word.

Hierdie vorms sluit in: ³

• Gewone breuk: teller is kleiner as noemer, byvoorbeeld 
• Onegte breuk – teller is groter as noemer, byvoorbeeld 
• Gemengde getal – heelgetal en ʼn gewone breuk saam geskryf, byvoorbeeld 5
• Desimale getalle/breuke – maak gebruik van ʼn komma om heelgetalle en gedeeltes van ʼn heelgetal van mekaar te skei, byvoorbeeld 5,34

Desimale getalle kan weer in eindigende en repeterende desimale getalle/breuke verdeel word. ² Eindigende desimale getalle kan uitgeskryf word tot op die laaste desimaal, byvoorbeeld 2,5. Repeterende desimale kan nie noodwendig uitgeskryf word tot op die laaste desimaal nie, maar volg ʼn bepaalde patroon wat veroorsaak dat ons weet wat die laaste desimaal sal wees, byvoorbeeld:

3,13333 = 3,1. Die kolletjie op die honderdstes sê vir ons dat daardie 3 vir ʼn onbepaalde lengte aanhou.

Heelgetalle

Heelgetalle is die getalle wat nie in kleiner dele opgedeel is nie. Hierdie getalle kan verder verdeel word in twee verskillende kategorieë, naamlik negatiewe getalle en natuurlike getalle. ⁴

Negatiewe getalle

Negatiewe getalle is getalle wat kleiner as nul is. Hierdie getalle lê dus links van nul op die getallelyn. Wanneer jy met negatiewe getalle werk, is dit belangrik om te weet dat jy links op die getallelyn moet beweeg. Onthou ook dat negatief en aftrek nie dieselfde ding is nie. “Negatief” verwys na ʼn tipe heelgetal, terwyl “aftrek” na ʼn tipe bewerking wat gedoen moet word, verwys. ⁵

Telgetalle

Natuurlike getalle is al die oorblywende heelgetalle. Hierdie getalle kan verder in nul en natuurlike getalle verdeel word. Nul is dus ʼn heelgetal wat heeltemal op sy eie staan. ²

Nul

Nul word in wiskunde as ʼn plekhouer of om die afwesigheid van ʼn waarde aan te dui, gebruik. Nul is ook die syfer wat op die getallelyn wat die positiewe getalle van die negatiewe getalle skei. ⁶

Natuurlike getalle

Natuurlike getalle is al die positiewe heelgetalle.

Natuurlike getalle word ook in verskillende subgetalle verdeel, naamlik: ²

• Ewe getalle
• Onewe getalle
• Priemgetalle
• Saamgestelde getalle
• Kwadraatgetalle
• Derdemagsgetalle

Ewe getalle

Ewe getalle is alle natuurlike getalle wat deur twee gedeel kan word en ʼn natuurlike getal as antwoord oplewer. Daar mag dus geen res in jou antwoord wees wanneer jy die deelbewerking doen nie. ⁷

Onewe getalle

Onewe getalle is alle natuurlike getalle wat ʼn breuk as antwoord oplewer wanneer die getal deur twee gedeel word. Daar sal dus ʼn res in jou antwoord oorbly wanneer jy die deelbewerking doen. ⁶

Priemgetalle

ʼn Priemgetal is ʼn getal wat slegs twee faktore het: 1 en die getal self. ʼn Priemgetal is dus ʼn getal wat slegs deur homself en 1 gedeel kan word en steeds ʼn natuurlike getal as antwoord gee. Priemgetalle kan dus deur geen ander getal gedeel word sonder om ʼn res in jou antwoord te kry nie. ⁷

Saamgestelde getalle

ʼn Saamgestelde getal is ʼn getal wat meer as twee faktore het. ʼn Saamgestelde getal kan dus deur meer as twee getalle gedeel word en ʼn natuurlike getal as antwoord gee. Onthou dat 1 nie ʼn saamgestelde of priemgetal is nie, aangesien 1 slegs een faktor het, naamlik 1. ²

Kwadraatgetalle

Kwadraatgetalle is die resultaat van ʼn getal wat met homself vermenigvuldig is. Voorbeelde hiervan is 1, 4, 9, 16, ens. Dit beteken: 1 x 1 = 1; 2 x 2 = 4; 3 x 3 = 9, ens. Die oorspronklike getalle wat met hulself vermenigvuldig word om kwadraatgetalle op te lewer, word vierkantswortels genoem. ⁵

Derdemagsgetalle

Derdemagsgetalle is die resultaat van ʼn getal wat drie keer met homself vermenigvuldig word. Voorbeelde hiervan is 1, 8, 27, ens. Dit beteken: 1 x 1 x 1 = 1; 2 x 2 x 2 = 8; 3 x 3 x 3 = 27, ens. Die oorspronklike getalle wat met hulself vermenigvuldig word om die derdemagsgetalle op te lewer, word derdemagswortels genoem. ⁵

Woordbank

teller	Die syfer wat bo staan in ʼn breuk; dit dui aan hoeveel stukkies daar is.
noemer	Die syfer wat onder staan in ʼn breuk; dit dui aan hoeveel ewe groot dele die heel verdeel is.
res	Die waarde wat oorbly nadat jy twee getalle met mekaar gedeel het wat nie volledig deelbaar is nie. As ek 7 lekkers het en ek deel dit tussen 2 maats, kry elke maat 3 lekkers en 1 lekker bly oor. Daardie 1 lekker is jou res waarde.
faktore	ʼn Getal wat presies in ʼn ander getal kan indeel sonder dat daar ʼn res oorbly. 3 is dus ʼn faktor van 12 want 12 ÷ 3 = 4.